
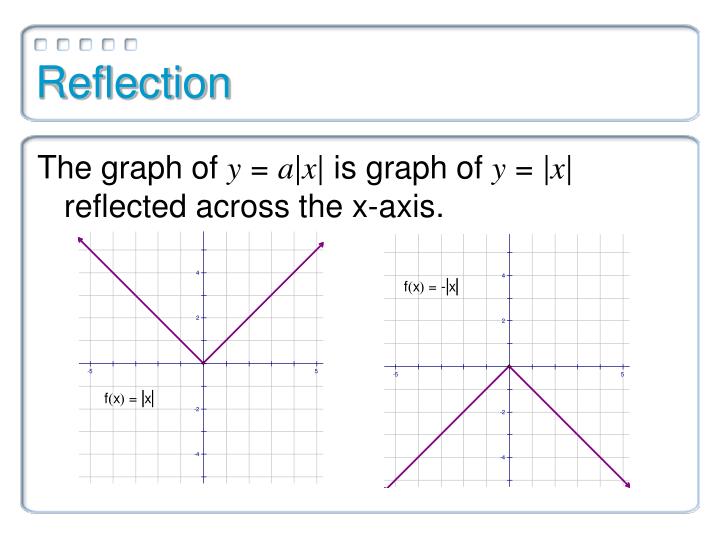
Determine the number of lines of symmetry.The figure in question is reflected over the x-axis. its left and right sides swapped from the original graph its been reflected across the y-axis. A reflection over the x-axis is a reflection in which the line of reflection is the x-axis. Describe the reflection by finding the line of reflection. The previous reflection was a reflection in the x-axis.Where should you park the car minimize the distance you both will have to walk? You need to go to the grocery store and your friend needs to go to the flower shop. Now we all know that the shortest distance between any two points is a straight line, but what would happen if you need to go to two different places?įor example, imagine you and your friend are traveling together in a car.
Looking again at A$^\prime$ and A$^$ its midpoint lies at the origin (0,0), and the same is true for all other points.And did you know that reflections are used to help us find minimum distances? The same calculations work for the other points: in each case, the $x$-coordinate does not change and the $y$-coordinate changes sign.īelow is a picture of the original points, their reflections over the $x$-axis and then the reflections of the new points over the $y$-axis:
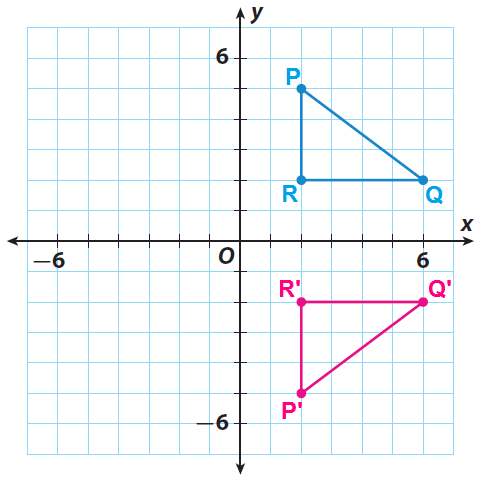
If we were to fold the plane along the $x$-axis, the points A and A$^\prime$ match up with one another. Notice that the lines extending from one point to. Reflecting over the $x$-axis does not change the $x$-coordinate but changes the sign of the $y$-coordinate. Reflections in the Coordinate Plane: Reflecting over the x-axis: (the x-axis as the line of reflection). Similarly the coordinates of $B$ are $(-4,-4)$ while $C = (4,-2)$ and $D = (2,1)$.īelow is a picture of the reflection of each of the four points over the $x$-axis: We can understand this concept using the function f (x)x+1 f (x) x +1. A reflection is equivalent to flipping the graph of the function using the axes as references. The reflections of a function are transformations that make the graph of a function reflected over one of the axes. The line is called the axis of reflection. Reflecting a function over the x -axis and y -axis.
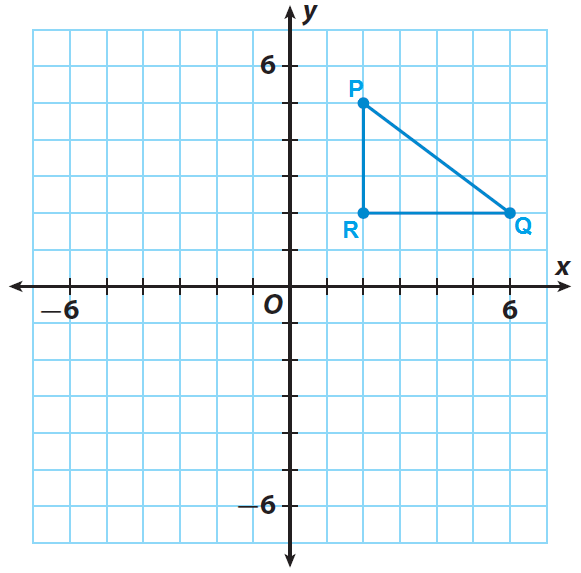
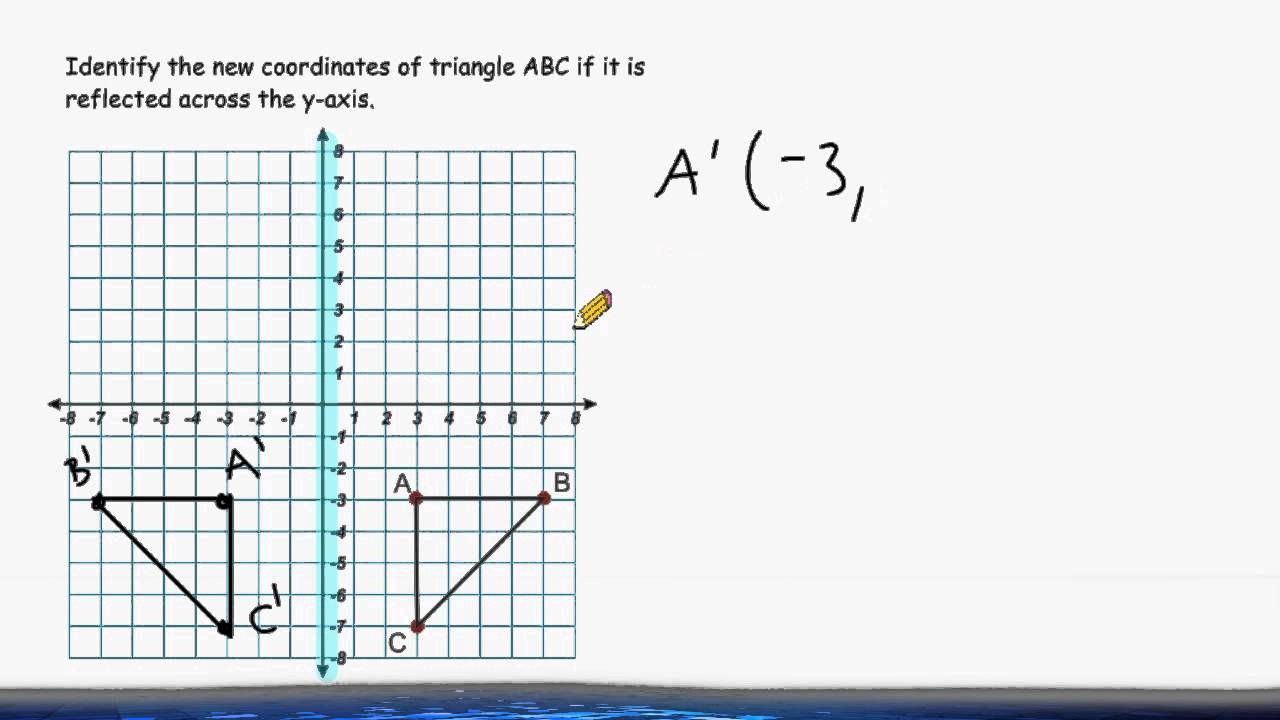
The coordinates of $A$ are $(-5,3)$ since $A$ is five units to the left of intersection of the axes and  3 units up. A reflection is a transformation that flips a figure over a line. Reflection across the x-axis: y -f(x) Pick three points with x and y value and graph Pick three points and graph Divide y values by -1 while x values stay. In order to help identify patterns in how the coordinates of the points change, the teacher may suggest for students to make a table of the points and their images after reflecting first over the $x$-axis and then over the $y$-axis: Point Thus the knowledge gained in this task will help students when they study transformations in the 8th grade and high school. Whenever you reflect a figure across a line of reflection that is also a line of symmetry. Later students will learn that this combination of reflections represents a 180 degree rotation about the origin. This means that if we reflect over the $x$-axis and then the $y$-axis then both coordinates will change signs.


 0 kommentar(er)
0 kommentar(er)
